Post

포켓몬고 Gamepress DPS 성능 계산 공식 분석

Posted Updated
By LeeGo
33 min read

포켓몬고의 레이드 배틀에서 최고의 성능을 발휘하는 포켓몬은 어떻게 선택해야 할까? 간략히 말하자면 포켓몬의 종류(스탯, 속성), 기술(위력, 속성) 등 다양한 요소를 고려해야 한다. 다행히 시뮬레이션을 통해 실전과 꽤 근접한 결과를 얻을 수 있다. 예를 들면 실제 시뮬레이션을 기반으로 직접 계산해 볼 수 있는 Poke Genie 앱, Poke Battler 사이트, Gamepress 사이트 등이 있다. 물론 여러 인포그래픽, 블로그, 유튜브를 통해서도 레이드 성능에 대한 정보가 충분히 제공되고 있다.

이 글에서는 여러 곳에서 참조되는 Gamepress에서 사용하는 레이드 성능 계산 공식1을 자세히 살펴보고, 자료를 이해하는 방법을 알아본다. Gamepress에서 제공되는 기본 DPS에 대한 핵심 내용을 요약하면 다음과 같다.

  • 일반적인 레이드 성능을 판단하기에 유용하다.
  • 실제 시뮬레이션이 아닌 자체 유도 공식에서 도출된 성능이다.
  • 전투에 참여하는 포켓몬은 레벨 40, 개쳇값 100%로 가정한다.
  • 레벨 40, (기본 방어력 187 + 개쳇값 15) 정도의 방어력 스탯을 가지는 무속성 보스를 상대로 한다. 비슷한 방어력 스탯을 가진 포켓몬으로는 기라티나 오리진폼, 슈바르고, 무우마직이 있다.

배경지식

포켓몬고의 실제 대미지 계산 공식에는 다음과 같은 특성이 사용된다. 본문을 설명하기 위해 필요한 개념정도로 이해하고 넘어가면 충분하다.

  • 기본 스탯: 포켓몬고에서 정의하는 각 포켓몬의 고유한 기본 능력치이다. 즉 동일한 포켓몬은 모두 동일한 기본 스탯을 가지고 있다. 영어로는 보통 base stats이라고 불리며 공격력, 방어력, 체력 세 가지 스탯으로 구분되고 자연수 범주의 값을 가진다.

  • 개쳇값: 포켓몬고에서 포켓몬의 어떤 성능에 영향을 미치는 요소 중 임의로 결정되는 유일한 값이다. 영어로는 individual values라고 불리며 줄여서 IV라고 한다. 0~15 사이의 정숫값을 가지며 현재 시점에서 교환을 통해서만 다시 결정할 수 있다.

  • 포켓몬 레벨: 포켓몬의 강화 수준을 의미한다. 0.5레벨 단위마다 정해진 계숫값(레벨 계수)이 있고, 유효 스탯을 계산할 때 사용된다.

  • 유효 스탯: 포켓몬고의 CP 계산, 유효 대미지 계산 등 실제 계산에서 사용되는 값이다.

유효 스탯 = (기본 스탯 + 개쳇값) × 레벨 계수

  • 속성: 포켓몬 또는 기술에 부여된 속성을 의미한다. 현재 시점에서 총 18개의 속성이 있고 공수를 주고 받을 때 상성이 존재한다.

  • 일반 공격: 포켓몬의 기본 공격이다. 배틀 상황에서 빈 화면 어딘가를 터치하면 일반 공격이 입력된다. 일반 공격을 통해 차징 공격을 사용하기 위한 에너지를 얻을 수 있다.

  • 차징 공격: 포켓몬의 특수 공격이다. 배틀 상황에서 차징 에너지가 충분히 쌓여 차징 버튼이 활성화 되었을 때, 해당 버튼을 터치하면 입력된다. 레이드 배틀에서는 필요 에너지가 100, 50, 33인 세 가지로만 분류된다.

  • 에너지: 포켓몬이 차징 공격을 사용하기 위해 필요한 힘이다. 일반 공격을 사용할 때, 레이드 또는 체육관 배틀에서 상대로부터 피해를 입었을 때 그 절반만큼 충전된다. 모든 포켓몬은 에너지를 최대 100까지만 충전할 수 있다.

레벨 20의 피카츄를 예시로 들면 다음과 같다.

Pikachu피카츄

기본 스탯값개쳇값유효 스탯(레벨 계수=0.5974)
기본 공격11215(112+15)×0.5974 ≈ 75.87
기본 방어9610(96+10)×0.5974 ≈ 63.32
기본 체력11115(111+15)×0.5974 ≈ 75.27

용어

포켓몬고 성능 측정에서 사용되는 몇 가지 지표를 알아보자.

  • TDO: Total Damage Output의 약자로 상대에게 가한 ‘전체 피해량’으로 직역할 수 있다. 포켓몬이 살아있는 동안 상대에게 가한 누적 피해량 또는 누적 대미지로 이해할 수 있다.

  • DPS: Damage Per Second의 약자로 상대에게 ‘1초당 가하는 피해량’으로 직역할 수 있다. TDO를 살아있는 시간으로 나눈 값으로 정의되며 포켓몬이 살아있는 동안 상대에게 가하는 평균 화력정도로 이해할 수 있다.

  • EPS: Energy Per Second의 약자로 ‘1초당 얻거나 소모하는 에너지양’으로 직역할 수 있다. 일반 공격에서는 초당 얻을 수 있는 에너지양으로 해석되고, 차징 공격에서는 초당 소모한 에너지양으로 해석할 수 있다. 즉 차징 에너지 효율에 대한 지표이다.

  • 유효 대미지: 상대 포켓몬이 정해졌을 때, 모든 계산이 완료되어 실제 적용되는 대미지 값이다. 이 값만큼 피해를 가해 상대방의 체력을 줄일 수 있다.

입력값

여기서부터 실제 DPS 계산을 위한 내용이다. 우선 두 개의 입력값이 주어진다.

  • $x$: 레이드 배틀이 종료되었을 때 남아있는 포켓몬의 차징 에너지
  • $y$: 상대 포켓몬의 DPS

그리고 다음은 대미지 계산 공식에서 사용되는 변수들이다.

  • $FDmg$: 일반 공격 유효 대미지
  • $CDmg$: 차징 공격 유효 대미지
  • $FE$: 일반 공격 시 얻게되는 차징 에너지
  • $CE$: 차징 공격 시 소모되는 차징 에너지
  • $FDur$: 일반 공격 시 소모되는 시간 (시전 시간, 쿨다운 등)
  • $CDur$: 차징 공격 시 소모되는 시간 (시전 시간, 쿨다운 등)
  • $CDWS$: 차징 공격 중 대미지창(damage window)의 시작 시각
  • $Def$: 대상 포켓몬의 유효 방어력
  • $HP$: 대상 포켓몬의 유효 체력

위 변수를 조합하여 만든 몇 가지를 정의하여 나열하면 다음과 같다.

  • $FDPS$: 일반 공격에 대한 DPS, $FDmg \over FDur$
  • $FEPS$: 일반 공격에 대한 EPS로 일반 공격을 통해 초당 얻을 수 있는 차징 에너지, $FE \over FDur$
  • $CDPS$: 차징 공격에 대한 DPS, $CDmg \over CDur$
  • $CEPS$: 차징 공격에 대한 EPS로 차징 공격을 통해 초당 소모하는 차징 에너지, $CE \over CDur$

궁극적으로 측정하고자 하는 지표는 다음과 같다.

  • $DPS_{0}$: Cycle DPS. 차징 공격을 1회 사용할 만큼 에너지를 채우기 위해 일반 공격을 여러번 가하는 주기(cycle) 동안 계산되는 DPS이다.
  • $DPS$: 종합 DPS

공식

$DPS$

  • 일반적인 레이드 성능을 판단하기에 유용하다.
  • 실제 시뮬레이션이 아닌 자체 유도 공식에서 도출된 성능이다.
  • 전투에 참여하는 포켓몬은 레벨 40, 개쳇값 100%로 가정한다.
  • 레벨 40, (기본 방어력 187 + 개쳇값 15) 정도의 방어력 스탯을 가지는 무속성 보스를 상대로 한다. 비슷한 방어력 스탯을 가진 포켓몬으로는 기라티나 오리진폼, 슈바르고, 무우마직이 있다.

Gamepress에서 제안하고 있는 Comprehensive DPS 최종 공식이다. 서두에서 요약한 바와 같은 특징을 가지고 있다. 공식의 유도 과정은 다음 절에서 살펴보고, 해석은 Cycle DPS에 대한 고찰에서 확인할 수 있다.

\[DPS = DPS_0 + \frac{CDPS - FDPS}{CEPS + FEPS} \cdot (0.5 - \frac{x}{HP}) \cdot y\]

$DPS_0$

\[DPS_0 = \frac{FDPS \cdot CEPS + CDPS \cdot FEPS}{CEPS + FEPS}\]

이때 차징 에너지를 100만큼 필요로 하는 소위 1차징 공격은 $CEPS$ 대신 $CEPS’$으로 대체하여 패널티2를 부여한다. 차이점은 기존 $CEPS$ 공식에 일반 공격 에너지, 상대방의 DPS, 차징 공격의 대미지 창(CDWS)의 시작 시각 등을 고려해서 마치 1차징 공격의 필요 에너지가 100보다 더 많이 필요한 것처럼 보이도록 패널티를 부여하였다.

\[CEPS' = \frac{CE + 0.5 \cdot FE + 0.5y \cdot CDWS}{CDur}\]

DPS 이론

가정

Gamepress에서 제안하는 DPS 모델은 다음의 세 가지를 가정한다.

첫 번째. $FDPS < CDPS$

차징 공격의 DPS는 일반 공격의 DPS보다 항상 크다. 물론 몇 가지 예외가 있을 수 있는데, 팬텀을 상대로 일반 공격 염동력과 차징 공격 로킥을 DPS 관점에서 비교하면 일반 공격이 더 강하다. 이러한 경우를 DPS 계산 과정에서 FDPS와 DPS 중 높은 값을 택하면 문제를 완화시킬 수 있다.

두 번째, $x$ 와 $y$는 서로 독립 변수이다

이 문장은 상대의 DPS $y$는 한결 같고 내 포켓몬의 DPS $x$와는 무관하다는 것을 의미한다. 하지만 실전 상황 중 1인 체육관 배틀 또는 타임어택 레이드 배틀과 같은 상황에서는 성립되지 않는 가정이다. 포켓몬고의 메커니즘에 따르면 적군을 강한 화력으로 공격할수록 적의 차징 에너지가 더 빨리 충전되기 때문에 상대는 차징 공격을 더 많이 사용하게 될 것이다.

세 번째, 전투 중 낭비되는 시간은 없다

포켓몬이 전투 중일 때, 일반 공격이나 차징 공격의 쿨다운을 제외하고 가만히 서 있는 시간은 없다고 가정한다.

$DPS$ 공식 유도

우선 다음의 용어를 정의한다.

  • $n$: 포켓몬이 전투 중인 동안 사용하는 일반 공격 횟수
  • $m$: 포켓몬이 전투 중인 동안 사용하는 차징 공격 횟수
  • $T$: 포켓몬의 전투 시간 (살아있는 시간)

앞서 전투 중인 포켓몬은 가만히 있는 시간이 없다고 가정했기 때문에 다음과 같이 정의할 수 있다.

\[n \cdot FDur + m \cdot CDur = T \tag{1}\]

이 방정식은 (좌변) 일반 공격을 $n$회, 차징 공격을 $m$회 사용하는 동안의 시간은 (우변) 레이드 배틀에 참여한 포켓몬이 전투하는 시간 $T$와 동일하다는 의미이다.

차징 에너지는 일반 공격을 사용하거나 상대로부터 피해를 입을 때 충전된다. 전자는 일반 공격마다 정해진 값이 있고, 후자는 피해량의 절반만큼 충전된다. 이러한 메커니즘을 고려하면 다음과 같이 정의할 수 있다.

\[n \cdot FE + 0.5 HP = m \cdot CE + x \tag{2}\]

이 방정식의 의미는 (좌변) 레이드 배틀에 참여한 포켓몬이 일반 공격을 $n$회 사용하여 얻은 에너지와 기절할 때까지 피해를 입어 얻을 수 있는 차징 에너지(실제 체력의 절반)만큼을 더한 것은 (우변) 차징 공격을 $m$회 사용하여 소모한 에너지와 배틀이 끝났을 때 남아있는 차징 에너지 $n$을 더한 것과 같다. 여기엔 낭비된 에너지가 없다는 가정이 내포되어있다.

1차징 공격에 대한 패널티를 오버차징을 고려하여 정의한다. $CE$ 변수를 $CE’$으로 대체하여 마치 차징 에너지가 100보다 더 필요한 것처럼 조정하였다2.

\[CE' = CE + 0.5 FE + 0.5 y \cdot CDWS \tag{3}\]

위에서 정의한 식 (1), (2)에 대해 $n$과 $m$을 미지수로 놓고 선형계 $Ax=b$ 형태로 풀어내면 다음과 같다.

\[\begin{bmatrix} FDur & CDur \\ FE & -CE \end{bmatrix} \begin{bmatrix} n \\ m \end{bmatrix} = \begin{bmatrix} T \\ x - 0.5HP \end{bmatrix} \tag{4}\]

이때 $A$에 대한 역행렬 $A^{-1}$을 구하여 $x=A^{-1}b$를 계산하면 미지수 $x$에 해당하는 $n$과 $m$을 구할 수 있다.

\[\begin{bmatrix} n \\ m \end{bmatrix} = A^{-1} \begin{bmatrix} T \\ x - 0.5HP \end{bmatrix} \tag{5}\] \[A^{-1} = \frac{1}{FDur \cdot CE + FE \cdot CDur} \begin{bmatrix} CE & CDur \\ FE & -FDur \end{bmatrix} \tag{6}\]

이제 (5)에 (6)을 대입하여 정리하면 다음과 같다.

\[n = \frac{T \cdot CE + CDur \cdot (x - 0.5HP)}{FDur \cdot CE + CDur \cdot FE} \tag{7}\] \[m = \frac{T \cdot FE - FDur \cdot (x - 0.5HP)}{FDur \cdot CE + CDur \cdot FE} \tag{8}\]

마지막으로 DPS를 구하기 전에 다음과 같은 관계를 생각할 수 있다.

\[T = \frac{HP}{y} \tag{9}\]

이 식의 의미는 배틀에 참여한 포켓몬이 전투(생존)하는 시간 $T$는 이 포켓몬의 체력 $HP$를 적의 DPS인 $y$로 나눈 값과 같다는 뜻이다.

이제 DPS 공식을 유도하기 위해 앞서 정의한 내용을 상기해보자.

TDO: Total Damage Output의 약자로 상대에게 가한 ‘전체 피해량’으로 직역할 수 있다. 포켓몬이 살아있는 동안 상대에게 가한 누적 피해량 또는 누적 대미지로 이해할 수 있다.

DPS: Damage Per Second의 약자로 상대에게 ‘1초당 가하는 피해량’으로 직역할 수 있다. TDO를 살아있는 시간으로 나눈 값으로 정의되며 포켓몬이 살아있는 동안 상대에게 가하는 평균 화력정도로 이해할 수 있다.

이 정의를 식으로 표현하면 다음과 같다.

\[TDO = n \cdot FDmg + m \cdot CDmg \tag{10}\] \[DPS = \frac{TDO}{T} \tag{11}\]

DPS 공식 (11)에 (7), (8), (9), (10)을 대입하여 전개하면 최종적으로 다음과 같이 정리된다.

\[\therefore DPS = \frac{FDPS \cdot CEPS + CDPS \cdot FEPS}{CEPS + FEPS} + \frac{CDPS - FDPS}{CEPS + FEPS} \cdot (0.5 - \frac{x}{HP}) \cdot y \tag{12}\]

$DPS_{0}$에 대한 고찰

$DPS_{0}$ 공식 유도

$DPS_{0}$는 Simple cycle DPS라고 불리며 정의는 다음과 같다.

A “cycle” is a series of Fmoves, and then one Cmove. It is the damage per second you do on average throughput that cycle.

이것을 풀어서 이야기하면 차징 공격을 1회 사용할 만큼 에너지를 채우기 위해 일반 공격을 $k$회 가해야 한다고 하자. 이때 일반 공격 $k$회에 대한 누적 대미지 동안의 화력은 $FDPS$이고, 차징 공격 1회에 대한 화력은 $CDPS$이므로 이 cycle 동안의 평균 화력 $DPS_{0}$는 조화 평균(harmonic mean)으로 계산할 수 있다.

$DPS_{0}$를 구하는 것은 평균 속력을 구하는 개념과 동일하다. 예를 들어 거리 $S$를 왕복할 때 갈 때 속력은 $a$ km/h, 올 때 속력은 $b$ km/h로 주행한다면 이때의 평균 속력 $x$는 다음과 같이 조화 평균으로 구할 수 있다.

\[\frac{S}{a} + \frac{S}{b} = \frac{2S}{x}\] \[\therefore x = \frac{2ab}{a+b}\]

위 내용을 $DPS_{0}$에 대한 조화 평균 수식으로 표현하면 다음과 같다.

\[\frac{k \cdot FDmg}{FDPS} + \frac{CDmg}{CDPS} = \frac{k \cdot FDmg + CDmg}{DPS_{0}} \tag{13}\]

그리고 차징 공격을 1회 사용하기 위해 가해야 하는 일반 공격 횟수 $k$는 다음과 같다.

\[k = \frac{CE}{FE} \tag{14}\]

식 (13)에 (14)를 대입하여 $DPS_{0}$를 좌변에 두고 정리하면 다음과 같다.

\[\therefore DPS_0 = \frac{FDPS \cdot CEPS + CDPS \cdot FEPS}{CEPS + FEPS}\]

$DPS$와의 관계

DPS 공식을 상기하면 다음과 같다.

\[DPS = DPS_0 + \frac{CDPS - FDPS}{CEPS + FEPS} \cdot (0.5 - \frac{x}{HP}) \cdot y\]

이 공식이 내포하고 있는 몇 가지 의미를 살펴보자.

  1. $y=0$ 이라면, 즉 레이드 보스가 공격을 하지 않아 가만히 있고, 전투가 영원히 지속된다면 $DPS=DPS_{0}$로 수렴하게 된다.
  2. $DPS$ 공식을 보면 다음과 같은 항이 있다. $\frac{CDPS - FDPS}{CEPS + FEPS}$ 이 항은 차징 에너지 효율을 의미하며, 첫 번째 가정 $FDPS < CDPS$에 의해 항상 0보다 크다.
  3. 일반적으로 레이드 보스가 가만히 있는 경우는 없으므로 $y>0$이고, 차징 에너지 효율도 항상 0보다 크다. 따라서 $DPS$ 공식에 따르면 $DPS$와 $DPS_{0}$는 $(0.5HP - x)$의 부호에만 영향을 받는다.
    • $x > 0.5HP$ 라면, 즉 전투 중인 포켓몬이 기절하는 시점에 남아있는 차징 에너지가 입은 피해로 인해 충전된 차징 에너지보다 많다면 $DPS < DPS_{0}$ 이다. 피해량으로 충전된 차징 에너지가 쓰이지 않고 낭비되었다는 의미다.
    • $x < 0.5HP$ 라면, 즉 전투 중인 포켓몬이 기절하는 시점에 남아있는 차징 에너지가 입은 피해로 인해 충전된 차징 에너지보다 적다면 $DPS > DPS_{0}$ 이다. 피해량으로 충전된 차징 에너지가 크게 낭비되지는 않았다는 의미다.

적용

Gamepress는 앞서 정의된 DPS 공식을 이용하여 전체 테이블을 만들고자 했다. 입력값은 두 개의 독립변수 $x$, $y$ 를 이용하여 함수 $DPS(x, y)$로 표현하고 싶었나보다. 이를 위해 두 가지 가정을 추가하였다.

가정

첫 번째, $x$와 $y$는 서로 독립적이다

전수 조사를 진행했을 때 일반화 할 수 있을 만한 가정이라고 한다. 물론 소수의 표본에서는 $x$가 $y$에 상관관계를 보이는 경향이 있다고 하지만 Gamepress에서 제안하고자 하는 Comprehensive DPS의 목적 자체가 “일반적인 성능”이기 때문에 이러한 가정이 충분히 유효하다고 판단한 듯 하다.

두 번째, 모든 다른 항들은 $x$, $y$와 독립적이다

여기서부터 이하의 내용은 어떻게 유도된 것인지 이해하지 못했다. basing on emperical simulation data 라고 하는 걸 보면 말 그대로인 것 같기도 하다.

일반적인 보스에 대한 성능 측정: 임의의 보스를 가정한다.

Gamepress를 기반으로 하는 모든 데이터들은 아래의 공식을 따라 $x$와 $y$값이 계산된다.

\[\begin{cases} E[x] = 0.5 CE + 0.5 FE \\ E[y] = \frac{900}{Def} \end{cases}\]
구체적인 보스에 대한 성능 측정: 특정 보스를 설정한다.

Gamepress에서 보스를 설정했을 땐 아래의 공식을 따라 $x$와 $y$값이 계산된다.

\[\begin{cases} E[x] = 0.5 CE + 0.5 FE + 0.5 \frac{ \lambda \cdot FDmg_{enemy} + CDmg_{enemy} } { \lambda + 1 } \\ E[y] = \frac{ \lambda \cdot FDmg_{enemy} + CDmg_{enemy} } { \lambda \cdot (FDur_{enemy} + 2) + CDur_{enemy} + 2 } \end{cases}\]
  • $ \lambda = 3 $, 상대 보스가 1차징 공격을 가지고 있는 경우
  • $ \lambda = 1.5 $, 상대 보스가 2차징 공격을 가지고 있는 경우
  • $ \lambda = 1 $, 상대 보스가 3차징 공격을 가지고 있는 경우

Gamepress에서는 DPS를 계산하여 커다란 테이블을 만들 때, 속도 향상을 위해서 유효 대미지 계산 중 $floor() + 1$을 사용하지 않는다. 대신에 유효 대미지 계산에서 많은 연산 자원을 잡아먹는 소숫점 계산 함수 $floor()$를 제외하고, $+1$ 대신 $+0.5$를 사용한다.

원래 유효 대미지 공식

\[floor(0.5 \cdot \frac{Atk}{Def} \cdot Power \cdot Modifier) + 1\]

Gamepress에서 사용하는 수정된 유효 대미지 공식

\[(0.5 \cdot \frac{Atk}{Def} \cdot Power \cdot Modifier) + 0.5\]

예시

앞서 소개한 피카츄를 레벨 40의 100% 개체로 하여 공식을 적용해보자. 스킬은 전기쇼크와 와일드볼트를 가지고 있다.

Pikachu피카츄

기본 스탯값개쳇값유효 스탯(레벨 계수=0.7903)
기본 공격11215(112+15)×0.7903 ≈ 100.37
기본 방어9615(96+15)×0.7903 ≈ 87.72
기본 체력11115(111+15)×0.7903 ≈ 99.58
  • $x = \frac{FE + CE}{2} = \frac{8 + 50}{2} = 29.000$
  • $y = \frac{900}{Def} = \frac{900}{87.72} ≈ 10.260$

그리고 다음은 대미지 계산 공식에서 사용되는 변수들이다.

  • \[FDmg = 0.5 \cdot (\frac{나의 유효 공격력(100.37)}{상대 유효 방어력(160)}) \cdot 전기쇼크 위력(5) \cdot 자속성(1.2) + 0.5 ≈ 2.382\]
  • \[CDmg = 0.5 \cdot (\frac{나의 유효 공격력(100.37)}{상대 유효 방어력(160)}) \cdot 와일드볼트 위력(90) \cdot 자속성(1.2) + 0.5 ≈ 34.374\]
  • $FE = 8$
  • $CE = 50$
  • $FDur = 0.6$
  • $CDur = 2.6$
  • $CDWS = 1.7$
  • $Def = 87.72$
  • $HP = 99.58$

위 변수를 조합하여 만든 몇 가지를 정의하여 나열하면 다음과 같다.

  • $FDPS = \frac{FDmg}{FDur} = \frac{2.382}{0.6} ≈ 3.970 $
  • $FEPS = \frac{FE}{FDur} = \frac{8}{0.6} ≈ 13.333$
  • $CDPS = \frac{CDmg}{CDur} = \frac{34.374}{2.6} ≈ 13.221 $
  • $CEPS = \frac{CE}{CDur} = \frac{50}{2.6} ≈ 19.231$

$DPS_{0}$와 $DPS$를 구해보자.

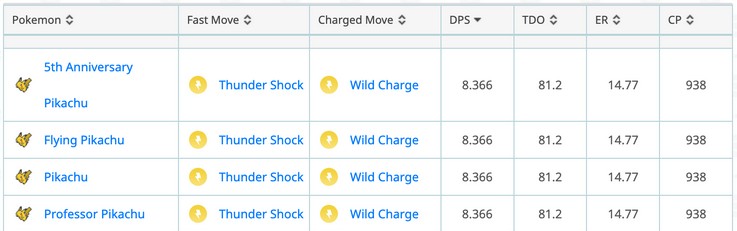
\[DPS_0 = \frac{FDPS \cdot CEPS + CDPS \cdot FEPS}{CEPS + FEPS} = \frac{3.970 \cdot 19.231 + 13.221 \cdot 13.333}{19.231 + 13.333} ≈ 7.758\] \[DPS = DPS_0 + \frac{CDPS - FDPS}{CEPS + FEPS} \cdot (0.5 - \frac{x}{HP}) \cdot y = 7.758 + \frac{13.221 - 3.970}{19.231 + 13.333} \cdot (0.5 - \frac{29}{99.58}) \cdot 10.260 ≈ 8.366\]

최종 계산된 결과는 DPS = 8.366이다. 아래 Gamepress에서 제공하는 표의 DPS 결과와 일치하는 것을 확인할 수 있다.

Pikachu-dps

마치며

이번 글에서는 포켓몬고의 레이드 배틀, 체육관 배틀에 참여할 때 포켓몬의 성능을 나타내는 지표에 대해서 다루었다. TDO는 포켓몬의 전투 시간 동안 가한 누적 대미지이므로 맷집에 대한 영향이 반영되어 있고, DPS는 포켓몬의 전투 시간 동안 평균적으로 가하는 대미지 수준을 나타낸다. 따라서 이러한 지표를 통해 서로 다른 포켓몬, 서로 다른 스킬 간에 상대적인 값을 비교하여 성능을 판단할 수 있다.

Gamepress에서 제공하는 DPS는 꽤 오래 전부터 통용되었다. 다시 본문을 읽어보아도 분석이 나름 근거가 있고 의미가 담겨있는 공식으로 보인다. 물론 요즘에는 좋은 실전 시뮬레이션이 나오긴 했지만 “일반적인 성능”을 가늠하기에는 Comprehensive DPS가 아직까지 충분히 유효해 보인다.

참고

  1. How to Calculate Comprehensive DPS, GamePress, link ↩︎

  2. 1차징 공격의 경우 에너지를 가득 채워야 차징 공격이 가능하다. 레이드 배틀의 성능은 차징 공격을 자주 사용할 수 있어야 높게 쳐줄 수 있는데, 1차징 공격은 에너지를 채우다가 죽기 십상이고, 100을 넘어간 오버차징 에너지는 낭비되기 때문에 이것을 고려한 패널티를 유도 공식에 적용한다. “1차징 용성군 vs 2차징 역린”을 비교하며 자주 화두에 오른다. Is Draco Meteor better than Outrage on Dragonite? ↩︎ ↩︎2

포켓몬고, 분석
PokemonGo DPS gamepress
This post is licensed under CC BY 4.0 by the author.