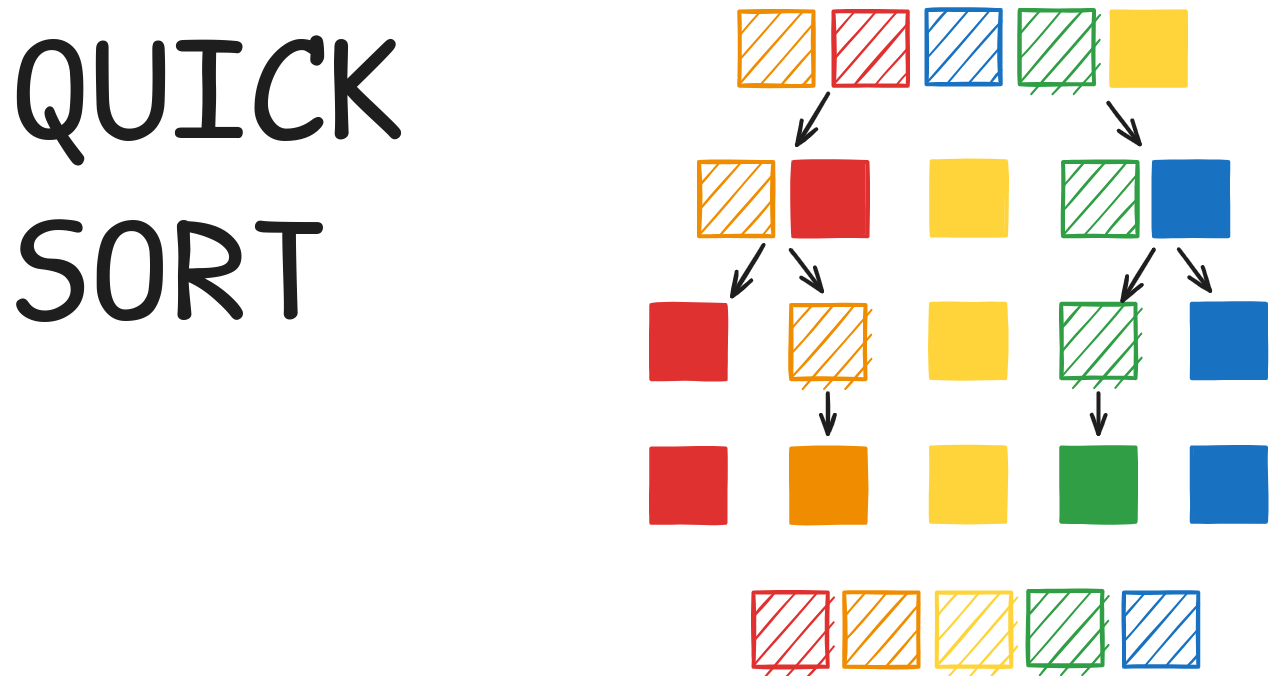
퀵 정렬(Quick Sort)

정의

퀵 정렬(Quick Sort)은 분할 정복(Divide and Conquer) 알고리즘에 기반한 정렬 알고리즘입니다. 퀵 정렬은 병합 정렬(Merge Sort)과 마찬가지로 배열을 재귀적으로 분할하지만 병합 단계 없이 분할 과정에서 정렬을 수행한다는 점이 다릅니다. 이는 퀵 정렬이 매우 빠르고 공간 효율적이게 만드는 주요 특징 중 하나입니다.

알고리즘 단계

1. 피벗 선택(Pivot Selection)

   • 배열에서 하나의 원소를 피벗(pivot)으로 선택합니다. 피벗 선택 방법은 다양하며 보통 첫 번째, 마지막, 중간 원소, 또는 무작위로 선택하는 방식이 사용됩니다.

2. 분할(Partition)

   • 피벗을 기준으로 배열을 두 개의 하위 배열로 분할합니다. 피벗보다 작은 원소들은 피벗의 왼쪽 하위 배열로 옮기고, 피벗보다 큰 원소들은 오른쪽 하위 배열로 옮깁니다. 피벗은 최종적으로 두 하위 배열 사이의 올바른(정렬된) 위치에 놓이게 됩니다.

3. 재귀적 정렬(Recursive Sort)

   • 분할된 두 하위 배열에 대해 재귀적으로 퀵 정렬을 수행합니다.

4. 정렬 완료

   • 재귀 호출이 완료되면 모든 하위 배열이 정렬되고, 전체 배열이 정렬된 상태가 됩니다.

Pseudo Code

def QUICK_SORT(array, low, high)
    if low < high:
        pivotIndex = PARTITION(array, low, high)
        QUICK_SORT(array, low, pivotIndex - 1)
        QUICK_SORT(array, pivotIndex + 1, high)

def PARTITION(array, low, high)
    pivot = array[high]  # Choose the last element as the pivot
    i = low
    j = high - 1 # Exclude the element at the pivot
    
    while True:
      # Move each index
      while i <= high - 1 and pivot >= array[i]:
         i = i + 1
      while j >= low and pivot <= array[j]:
         j = j + 1

      # Exchange the elements at each index
      if i > j:
         swap array[i] with array[high]
         return i
      else:
         swap array[i] with array[j]

위 분할(partition) 알고리즘¹²은 Tony Hoare³이 제안한 방법입니다. 피벗이 배열의 어느 위치에 선택되었는지에 따라 low 또는 high 포인터와의 교환이 결정됩니다. 본문에서는 마지막 요소가 피벗인 경우를 기준으로 하고 있습니다.

• 마지막 요소가 피벗일 때: low 포인터와 교환
• 첫 번째 요소가 피벗일 때: high 포인터와 교환
• 중간 요소가 피벗일 때: 상황에 따라 low 또는 high 포인터와 교환

성능

시간 복잡도

퀵 정렬의 시간 복잡도는 피벗 선택 방법과 데이터의 분포에 따라 다릅니다.

1. 최선의 경우(Best Case): $O(n\log_2 n)$

   • 피벗이 항상 배열의 중앙에 가까운 경우 배열이 매번 균등하게 분할되어 로그 깊이의 재귀 호출이 필요합니다.

2. 평균의 경우(Average Case): $O(n\log_2 n)$

   • 대부분의 경우 피벗이 배열을 적당히 균등하게 분할하기 때문에 로그 깊이의 재귀 호출이 필요합니다.

3. 최악의 경우(Worst Case): $O(n^2)$

   • 피벗이 배열의 최댓값이나 최솟값으로 선택되어 배열이 최대한 불균형하게 분할되는 경우입니다. 예를 들어 이미 정렬된 배열에 대해 첫 번째 또는 마지막 원소를 항상 피벗으로 선택하면 최악의 성능을 보입니다.

공간 복잡도

퀵 정렬은 추가적인 메모리를 거의 사용하지 않고 제자리에서(in-place) 정렬을 수행합니다. 그러나 재귀 호출 스택만큼의 추가 공간이 필요합니다.

1. 최선, 평균의 경우: $O(\log_2 n)$
2. 최악의 경우: $O(n)$

예시

문제

block-beta
    columns 9
        2 1 5 4 3

피벗 선택

마지막 원소를 피벗으로 선택하는 방식을 취한다. 초기에 선택되는 피벗의 값은 3이다.

분할

피벗보다 작은 원소들은 피벗의 왼쪽 하위 배열에, 피벗보다 큰 원소들은 오른쪽 하위 배열에 위치시킨다.

• pivot: 위 문장과 같이 피벗을 중심으로 원소들의 크기가 좌우로 정렬된다. 아래의 풀이에서 초록색으로 표기된다.

• low: 피벗을 제외한 가장 왼쪽에 위치한 지점을 초깃값으로 가리키며 low 포인터 또는 마커라고 불린다. 아래의 풀이에서 빨간색으로 표기된다. 피벗보다 큰 값을 만날 때까지 오른쪽으로 이동한다.

• high: 피벗을 제외한 가장 오른쪽에 위치한 지점을 초깃값으로 가리키며 high 포인터 또는 마커라고 불린다. 아래의 풀이에서 파란색으로 표기된다. 피벗보다 작은 값을 만날 때까지 왼쪽으로 이동한다.

1

block-beta
    2 space 1 space 5 space 4 space 3
    style 4 fill:#3F53D2,color:#fff
    style 2 fill:#D02519,color:#fff
    style 3 fill:#80A924,color:#fff

block-beta
    2 space 1 space 5 space 4 space 3
    2 --> 5
    style 4 fill:#3F53D2,color:#fff
    style 5 fill:#D02519,color:#fff
    style 3 fill:#80A924,color:#fff

block-beta
    2 space 1 space 5 space 4 space 3
    4 --> 1
    style 1 fill:#3F53D2,color:#fff
    style 5 fill:#D02519,color:#fff
    style 3 fill:#80A924,color:#fff

block-beta
    2 space 1 space 5 space 4 space 3
    3 --> 5
    5 --> 3
    style 1 fill:#3F53D2,color:#fff
    style 5 fill:#D02519,color:#fff
    style 3 fill:#80A924,color:#fff

block-beta
    2 space 1 space 3 space 4 space 5
    style 3 fill:#A7AEB4,color:#fff

2

block-beta
    2 space 1 space 3 space 4 space 5
    1 --> 2
    2 --> 1
    style 3 fill:#A7AEB4,color:#fff
    style 2 fill:#D02519,color:#fff
    style 1 fill:#80A924,color:#fff

block-beta
    1 space 2 space 3 space 4 space 5
    style 3 fill:#A7AEB4,color:#fff
    style 1 fill:#A7AEB4,color:#fff

block-beta
    1 space 2 space 3 space 4 space 5
    style 3 fill:#A7AEB4,color:#fff
    style 1 fill:#A7AEB4,color:#fff
    style 2 fill:#A7AEB4,color:#fff

3

block-beta
    1 space 2 space 3 space 4 space 5
    style 3 fill:#A7AEB4,color:#fff
    style 1 fill:#A7AEB4,color:#fff
    style 2 fill:#A7AEB4,color:#fff
    style 5 fill:#80A924,color:#fff
    style 4 fill:#3F53D2,color:#fff

block-beta
    1 space 2 space 3 space 4 space 5
    style 3 fill:#A7AEB4,color:#fff
    style 1 fill:#A7AEB4,color:#fff
    style 2 fill:#A7AEB4,color:#fff
    style 5 fill:#A7AEB4,color:#fff

block-beta
    1 space 2 space 3 space 4 space 5
    style 3 fill:#A7AEB4,color:#fff
    style 1 fill:#A7AEB4,color:#fff
    style 2 fill:#A7AEB4,color:#fff
    style 5 fill:#A7AEB4,color:#fff
    style 4 fill:#A7AEB4,color:#fff

정렬 완료

block-beta
    1 2 3 4 5

참고

1. Cormen, Thomas H, Charles Eric Leiserson, and Ronald L Rivest. “7 Quicksort,” in Introduction to Algorithms. 4th ed. 182-204 Cambridge, Mass.: Mit Press, 2022. ↩︎

2. 윤성우, “10장. 정렬(sorting)” in 윤성우의 열혈 자료구조: C언어를 이용한 자료구조 학습서, 오렌지미디어(2012) ↩︎

3. 위키피디아, Tony Hoare, link ↩︎