시간 복잡도(Time Complexity)

정의

시간 복잡도(time complexity)는 알고리즘이 실행되는 동안 걸리는 시간을 입력 크기 $n$에 대한 함수 $T(n)$으로 표현한 것입니다. 즉 입력 크기가 증가할 때 알고리즘이 얼마나 빨리 실행될 수 있는지를 나타냅니다. 한 마디로 속도에 대한 평가 지표입니다.

표기법

시간 복잡도는 주로 빅 오 표기법(Big-O notation)을 사용하여 나타냅니다. 빅 오 표기법은 주어진 함수에서 입력 크기 $n$이 증가할 때 복잡도가 가장 빨리 증가하는 항만 고려하는 방법입니다. 다시 말해 주어진 시간 복잡도에 대한 수행 시간의 상한을 나타냅니다. 주의할 점은 이 정의가 특별히 최악의 수행 시간을 의미하는 것은 아니라는 사실입니다. 참고로 “빅 오”의 “오”는 Order의 첫 글자 O입니다.

예를 들어 다항식의 시간 복잡도 표기는 다음과 같습니다.

• $T(n) = a_m n^m + a_{m-1} n^{m-1} + … + a_1 n^1 + a_0$

• $O(T(n)) = O(n^m)$

빅 오 표기법 의미

빅 오 표기법은 함수의 상한선을 표현한다는 데 의미가 있습니다. $N$에 대한 함수 $f(N)$이 주어질 때, 등식 $f(N)=O(g(N))$은 다음을 의미합니다.

아주 큰 $N_0$와 $C(N_0, C>0)$를 적절히 선택하면 $N_0 \le N$인 모든 $N$에 대해 $|f(N)| \le C \times |g(N)|$이 참이 되도록 할 수 있다.
출처: 구종만, 알고리즘 문제 해결 전략 1, 인사이트(2012), p110

예를 들어 $f(N) = 3N + 2$의 시간 복잡도가 $O(N)$으로 표기되는지 확인해봅시다. 비교 함수로는 $g(N) = N$이 선택됩니다. 이때 조건을 만족하는 상수 $N_0$와 $C$를 구해봅시다. 우선 $N$과 $C$가 양수이기 때문에 절댓값 부호를 제거하고, 양변을 $N$으로 나누어 정리하면 다음과 같습니다.

\[|3N + 2| \le C \times |N| \tag{1}\] \[3 + \frac{2}{N} \le C \tag{2}\]

아주 큰 $N_0$를 표현하기 위해 $N \to \infty$인 경우를 생각해봅시다. 이때 식 (2)에서 $\frac{2}{N}$항은 $0$으로 수렴하므로 이 식은 $C \ge 3$로 정리됩니다. 다시 말해 아주 큰 $N_0$와 $3$이상의 $C$인 경우 위 조건이 항상 성립한다는 것을 알 수 있습니다.

적절한 $N_0=1$로 하여 $N \ge 1$인 경우를 생각해봅시다. 간단하게 $C \ge 5$로 정리됩니다. 그리고 아래의 식 (3), (4), (5)를 통해 위 정의가 성립하는 것을 차례로 확인할 수 있습니다.

\[N \ge 1 = N_0 \tag{3}\] \[C \ge 5 \tag{4}\] \[|3N + 2| \le 5 \times |N|\tag{5}\]

위 의미와 동일한 내용이지만 다른 책에서는 아래와 같이 정의하기도 합니다.

두 개의 함수 $f(n)$과 $g(n)$이 주어졌을 때, 모든 $n \ge K$에 대하여 $f(n) \le Cg(n)$을 만족하는 두 개의 상수 $C$와 $K$가 존재하면 $f(n)$의 빅-오는 $O(g(n))$이다.
출처: 윤성우, 열혈 자료구조, 오렌지미디어(2012), p42

빅 오 표기법 사례

차트

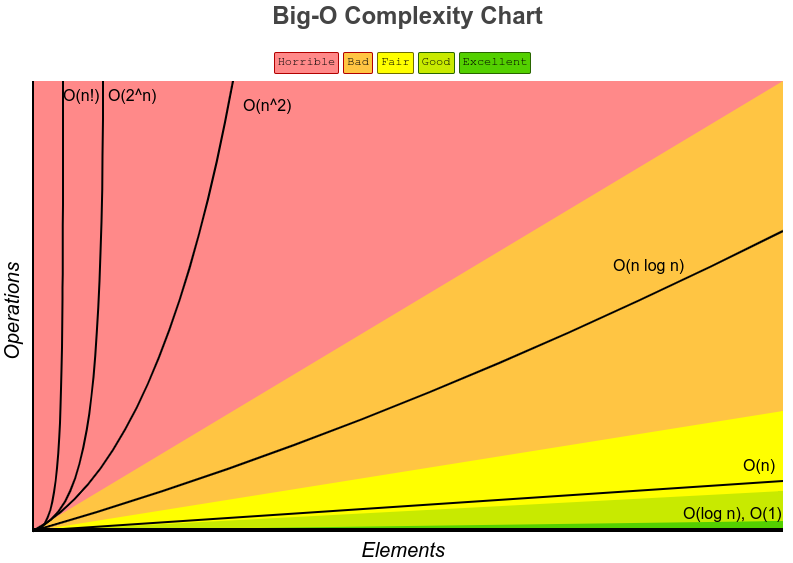출처: https://www.bigocheatsheet.com/

성능

비교

\[O(1) < O(\log n) < O(n) < O(n \log n) < O(n^2) < O(n^3) < O(2^n) < O(n!)\]

사례

$O(1)$

상수 시간(constant time) 복잡도. 입력 크기와 무관하게 수행 시간이 일정합니다. 예: 배열의 첫 번째 요소에 접근하기.

$O(\log n)$

로그 시간(logarithmic time) 복잡도. 입력 크기가 증가할수록 수행 시간이 증가하지만, 그 증가 속도가 매우 느립니다. 예: 이진 탐색.

$O(n)$

선형 시간(linear time) 복잡도. 입력 크기에 비례하여 시간이 증가합니다. 예: 배열에서 특정 요소 찾기.

$O(n\log n)$

선형 로그 시간(linearithmic time) 복잡도. 정렬 알고리즘에서 자주 나타납니다. 예: 퀵 정렬, 병합 정렬.

$O(n^2)$

이차 시간(quadratic time) 복잡도. 이중 루프가 있는 알고리즘에서 자주 나타납니다. 예: 버블 정렬, 삽입 정렬.

$O(n^3)$

삼차 시간(cubic time) 복잡도. 예: Naive multiplication of two $n \times n$ matrices, Calculating partial correlation

$O(2^n)$

지수 시간(exponential time) 복잡도. 매우 비효율적이며 입력 크기가 조금만 커져도 시간이 급격히 증가합니다. 예: 피보나치 수를 재귀적으로 계산하는 알고리즘.

$O(n!)$

팩토리얼 시간 복잡도. 매우 비효율적인 경우로, 주로 순열과 조합 문제에서 나타납니다.

참고

• 구종만, 알고리즘 문제 해결 전략 1, 인사이트(2012)
• 윤성우, 열혈 자료구조, 오렌지미디어(2012)